Skip to contents

Sensitivity of MLP models

Source: R/HessianMLP.R
HessianMLP.Rd

Function for evaluating the sensitivities of the inputs variables in a mlp model

Usage

HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  ...
)

# S3 method for default
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  trData,
  actfunc = NULL,
  deractfunc = NULL,
  der2actfunc = NULL,
  preProc = NULL,
  terms = NULL,
  output_name = NULL,
  ...
)

# S3 method for train
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  ...
)

# S3 method for H2OMultinomialModel
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  ...
)

# S3 method for H2ORegressionModel
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  ...
)

# S3 method for list
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  trData,
  actfunc,
  ...
)

# S3 method for mlp
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  trData,
  preProc = NULL,
  terms = NULL,
  ...
)

# S3 method for nn
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  preProc = NULL,
  terms = NULL,
  ...
)

# S3 method for nnet
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  trData,
  preProc = NULL,
  terms = NULL,
  ...
)

# S3 method for nnetar
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  ...
)

# S3 method for numeric
HessianMLP(
  MLP.fit,
  .returnSens = TRUE,
  plot = TRUE,
  .rawSens = FALSE,
  sens_origin_layer = 1,
  sens_end_layer = "last",
  sens_origin_input = TRUE,
  sens_end_input = FALSE,
  trData,
  actfunc = NULL,
  preProc = NULL,
  terms = NULL,
  ...
)

Arguments

MLP.fit

fitted neural network model

.returnSens

DEPRECATED

plot

logical whether or not to plot the analysis. By default is TRUE.

.rawSens

DEPRECATED

sens_origin_layer

numeric specifies the layer of neurons with respect to which the derivative must be calculated. The input layer is specified by 1 (default).

sens_end_layer

numeric specifies the layer of neurons of which the derivative is calculated. It may also be 'last' to specify the output layer (default).

sens_origin_input

logical specifies if the derivative must be calculated with respect to the inputs (TRUE) or output (FALSE) of the sens_origin_layer layer of the model. By default is TRUE.

sens_end_input

logical specifies if the derivative calculated is of the output (FALSE) or from the input (TRUE) of the sens_end_layer layer of the model. By default is FALSE.

...

additional arguments passed to or from other methods

trData

data.frame containing the data to evaluate the sensitivity of the model

actfunc

character vector indicating the activation function of each neurons layer.

deractfunc

character vector indicating the derivative of the activation function of each neurons layer.

der2actfunc

character vector indicating the second derivative of the activation function of each neurons layer.

preProc

preProcess structure applied to the training data. See also preProcess

terms

function applied to the training data to create factors. See also train

output_name

character name of the output variable in order to avoid changing the name of the output variable in trData to '.outcome'

Value

SensMLP object with the sensitivity metrics and sensitivities of the MLP model passed to the function.

Details

In case of using an input of class factor and a package which need to enter the input data as matrix, the dummies must be created before training the neural network.

After that, the training data must be given to the function using the trData argument.

Plots

  • Plot 1: colorful plot with the classification of the classes in a 2D map

  • Plot 2: b/w plot with probability of the chosen class in a 2D map

  • Plot 3: plot with the stats::predictions of the data provided

Examples

## Load data -------------------------------------------------------------------
data("DAILY_DEMAND_TR")
fdata <- DAILY_DEMAND_TR
## Parameters of the NNET ------------------------------------------------------
hidden_neurons <- 5
iters <- 100
decay <- 0.1

################################################################################
#########################  REGRESSION NNET #####################################
################################################################################
## Regression dataframe --------------------------------------------------------
# Scale the data
fdata.Reg.tr <- fdata[,2:ncol(fdata)]
fdata.Reg.tr[,3] <- fdata.Reg.tr[,3]/10
fdata.Reg.tr[,1] <- fdata.Reg.tr[,1]/1000

# Normalize the data for some models
preProc <- caret::preProcess(fdata.Reg.tr, method = c("center","scale"))
nntrData <- predict(preProc, fdata.Reg.tr)

#' ## TRAIN nnet NNET --------------------------------------------------------
# Create a formula to train NNET
form <- paste(names(fdata.Reg.tr)[2:ncol(fdata.Reg.tr)], collapse = " + ")
form <- formula(paste(names(fdata.Reg.tr)[1], form, sep = " ~ "))

set.seed(150)
nnetmod <- nnet::nnet(form,
                      data = nntrData,
                      linear.output = TRUE,
                      size = hidden_neurons,
                      decay = decay,
                      maxit = iters)
#> # weights:  21
#> initial  value 2487.870002 
#> iter  10 value 1587.516208
#> iter  20 value 1349.706741
#> iter  30 value 1333.940734
#> iter  40 value 1329.097060
#> iter  50 value 1326.518168
#> iter  60 value 1323.148574
#> iter  70 value 1322.378769
#> iter  80 value 1322.018091
#> final  value 1321.996301 
#> converged
# Try HessianMLP
NeuralSens::HessianMLP(nnetmod, trData = nntrData, plot = FALSE)
#> Sensitivity analysis of 2-5-1 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $.outcome
#> , , 1
#> 
#>            WD     TEMP
#> WD   1.028311 1.174910
#> TEMP 1.174910 3.386778
#> 
#> , , 2
#> 
#>             WD     TEMP
#> WD   -2.693044 0.856781
#> TEMP  0.856781 1.608223
#> 
#> , , 3
#> 
#>             WD      TEMP
#> WD   -3.523861 -2.061425
#> TEMP -2.061425 -5.352261
#> 
#> , , 4
#> 
#>             WD      TEMP
#> WD   -3.823715 -2.719650
#> TEMP -2.719650 -7.312955
#> 
#> , , 5
#> 
#>              WD      TEMP
#> WD   -2.1583991 0.4679963
#> TEMP  0.4679963 1.9635852
#> 
# \donttest{
# Try HessianMLP to calculate sensitivities with respect to output of hidden neurones
NeuralSens::HessianMLP(nnetmod, trData = nntrData,
                             sens_origin_layer = 2,
                             sens_end_layer = "last",
                             sens_origin_input = FALSE,
                             sens_end_input = FALSE)
#> Warning: All aesthetics have length 1, but the data has 15 rows.
#> ℹ Did you mean to use `annotate()`?
#> Warning: minimum occurred at one end of the range
#> Warning: minimum occurred at one end of the range
#> Warning: minimum occurred at one end of the range

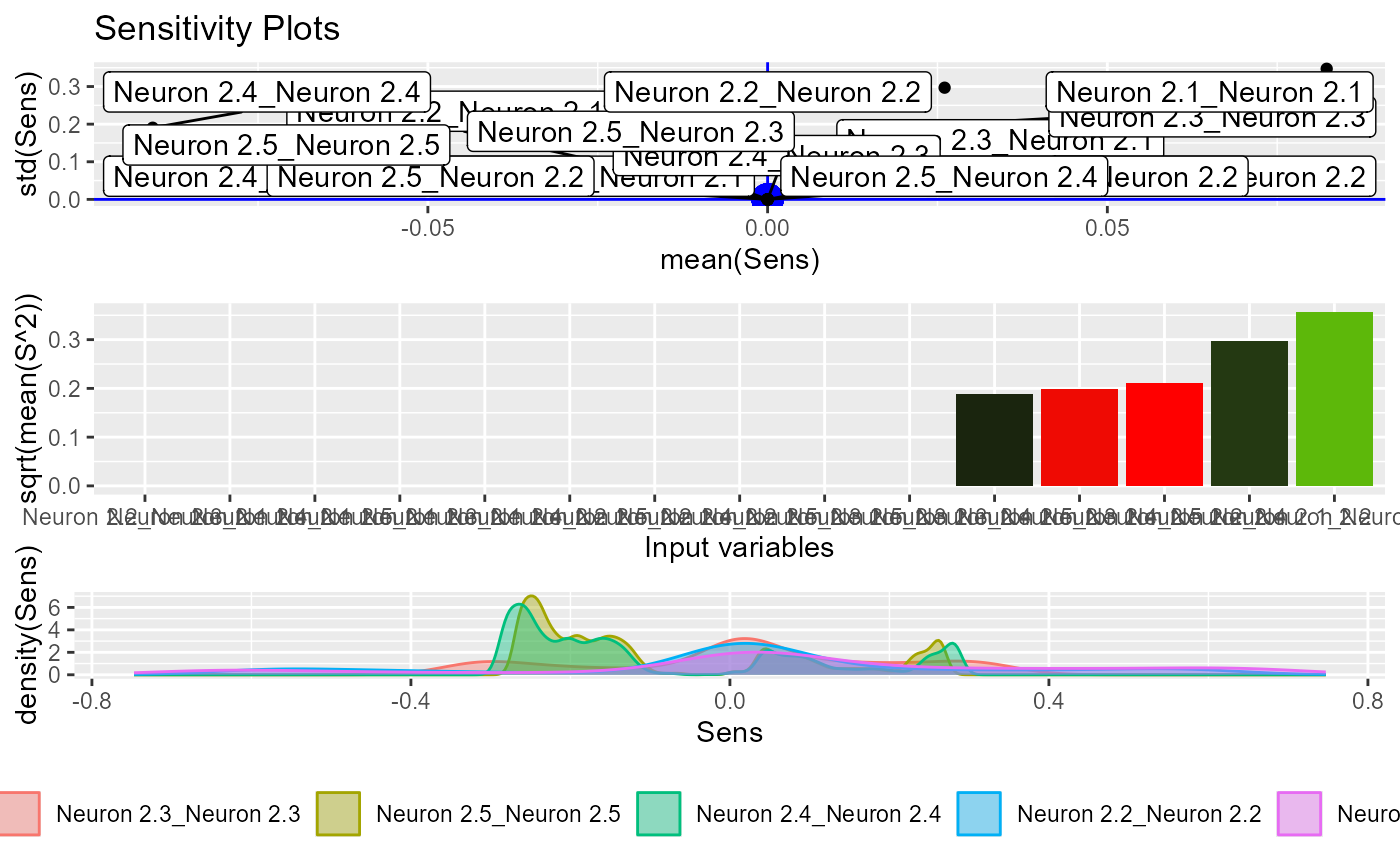#> Sensitivity analysis of 2-5-1 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $.outcome
#> , , 1
#> 
#>             Neuron 2.1 Neuron 2.2 Neuron 2.3 Neuron 2.4 Neuron 2.5
#> Neuron 2.1 0.001619946  0.0000000 0.00000000  0.0000000 0.00000000
#> Neuron 2.2 0.000000000  0.2446066 0.00000000  0.0000000 0.00000000
#> Neuron 2.3 0.000000000  0.0000000 0.02694284  0.0000000 0.00000000
#> Neuron 2.4 0.000000000  0.0000000 0.00000000  0.0483464 0.00000000
#> Neuron 2.5 0.000000000  0.0000000 0.00000000  0.0000000 0.04601234
#> 
#> , , 2
#> 
#>            Neuron 2.1 Neuron 2.2 Neuron 2.3 Neuron 2.4 Neuron 2.5
#> Neuron 2.1 0.03842943 0.00000000 0.00000000  0.0000000  0.0000000
#> Neuron 2.2 0.00000000 0.09207826 0.00000000  0.0000000  0.0000000
#> Neuron 2.3 0.00000000 0.00000000 0.02007891  0.0000000  0.0000000
#> Neuron 2.4 0.00000000 0.00000000 0.00000000 -0.2799695  0.0000000
#> Neuron 2.5 0.00000000 0.00000000 0.00000000  0.0000000 -0.2605999
#> 
#> , , 3
#> 
#>            Neuron 2.1 Neuron 2.2 Neuron 2.3 Neuron 2.4 Neuron 2.5
#> Neuron 2.1 0.04652198  0.0000000 0.00000000  0.0000000  0.0000000
#> Neuron 2.2 0.00000000 -0.4592029 0.00000000  0.0000000  0.0000000
#> Neuron 2.3 0.00000000  0.0000000 0.01420032  0.0000000  0.0000000
#> Neuron 2.4 0.00000000  0.0000000 0.00000000 -0.2499173  0.0000000
#> Neuron 2.5 0.00000000  0.0000000 0.00000000  0.0000000 -0.2360522
#> 
#> , , 4
#> 
#>            Neuron 2.1 Neuron 2.2  Neuron 2.3 Neuron 2.4 Neuron 2.5
#> Neuron 2.1 0.03074436  0.0000000 0.000000000  0.0000000  0.0000000
#> Neuron 2.2 0.00000000 -0.5986865 0.000000000  0.0000000  0.0000000
#> Neuron 2.3 0.00000000  0.0000000 0.008724927  0.0000000  0.0000000
#> Neuron 2.4 0.00000000  0.0000000 0.000000000 -0.2480003  0.0000000
#> Neuron 2.5 0.00000000  0.0000000 0.000000000  0.0000000 -0.2344207
#> 
#> , , 5
#> 
#>            Neuron 2.1 Neuron 2.2 Neuron 2.3 Neuron 2.4 Neuron 2.5
#> Neuron 2.1 0.09249169 0.00000000 0.00000000  0.0000000  0.0000000
#> Neuron 2.2 0.00000000 0.07461993 0.00000000  0.0000000  0.0000000
#> Neuron 2.3 0.00000000 0.00000000 0.02815211  0.0000000  0.0000000
#> Neuron 2.4 0.00000000 0.00000000 0.00000000 -0.2336736  0.0000000
#> Neuron 2.5 0.00000000 0.00000000 0.00000000  0.0000000 -0.2210683
#> 
## Train caret NNET ------------------------------------------------------------
# Create trainControl
ctrl_tune <- caret::trainControl(method = "boot",
                                 savePredictions = FALSE,
                                 summaryFunction = caret::defaultSummary)
set.seed(150) #For replication
caretmod <- caret::train(form = DEM~.,
                              data = fdata.Reg.tr,
                              method = "nnet",
                              linout = TRUE,
                              tuneGrid = data.frame(size = 3,
                                                    decay = decay),
                              maxit = iters,
                              preProcess = c("center","scale"),
                              trControl = ctrl_tune,
                              metric = "RMSE")
#> Loading required package: ggplot2
#> Loading required package: lattice
#> # weights:  13
#> initial  value 448.296994 
#> iter  10 value 4.240464
#> iter  20 value 2.955813
#> iter  30 value 2.432667
#> iter  40 value 2.152339
#> iter  50 value 2.119534
#> iter  60 value 2.116452
#> iter  70 value 2.115042
#> final  value 2.115024 
#> converged
#> # weights:  13
#> initial  value 259.256650 
#> iter  10 value 5.626711
#> iter  20 value 3.294659
#> iter  30 value 2.713958
#> iter  40 value 2.218022
#> iter  50 value 2.141379
#> iter  60 value 2.100764
#> iter  70 value 2.080285
#> iter  80 value 2.075813
#> iter  90 value 2.075489
#> final  value 2.075479 
#> converged
#> # weights:  13
#> initial  value 839.080081 
#> iter  10 value 7.558987
#> iter  20 value 5.177089
#> iter  30 value 4.017037
#> iter  40 value 2.214439
#> iter  50 value 2.059848
#> iter  60 value 2.054339
#> iter  70 value 2.045965
#> iter  80 value 2.039738
#> iter  90 value 2.015979
#> iter 100 value 1.990266
#> final  value 1.990266 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 2367.468092 
#> iter  10 value 18.231718
#> iter  20 value 6.058120
#> iter  30 value 3.242985
#> iter  40 value 2.187840
#> iter  50 value 2.071775
#> iter  60 value 2.050664
#> iter  70 value 2.028564
#> iter  80 value 2.004616
#> iter  90 value 1.984345
#> iter 100 value 1.979182
#> final  value 1.979182 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 466.520607 
#> iter  10 value 26.340684
#> iter  20 value 5.710540
#> iter  30 value 4.505050
#> iter  40 value 3.920448
#> iter  50 value 2.611841
#> iter  60 value 2.175444
#> iter  70 value 2.114173
#> iter  80 value 2.113462
#> iter  90 value 2.113367
#> final  value 2.113363 
#> converged
#> # weights:  13
#> initial  value 997.898260 
#> iter  10 value 7.946815
#> iter  20 value 3.796169
#> iter  30 value 2.732974
#> iter  40 value 2.185516
#> iter  50 value 2.016426
#> iter  60 value 1.996298
#> iter  70 value 1.984364
#> iter  80 value 1.983086
#> iter  90 value 1.983051
#> final  value 1.983051 
#> converged
#> # weights:  13
#> initial  value 926.945659 
#> iter  10 value 8.424427
#> iter  20 value 3.640577
#> iter  30 value 2.446188
#> iter  40 value 2.280445
#> iter  50 value 2.270542
#> iter  60 value 2.265967
#> iter  70 value 2.255105
#> iter  80 value 2.247681
#> iter  90 value 2.244869
#> iter 100 value 2.244534
#> final  value 2.244534 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 142.892088 
#> iter  10 value 6.910998
#> iter  20 value 5.724961
#> iter  30 value 4.789805
#> iter  40 value 3.951995
#> iter  50 value 2.271814
#> iter  60 value 2.143636
#> iter  70 value 2.081638
#> iter  80 value 2.053068
#> iter  90 value 2.050443
#> iter 100 value 2.050366
#> final  value 2.050366 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 224.855827 
#> iter  10 value 6.463371
#> iter  20 value 4.498606
#> iter  30 value 4.138860
#> iter  40 value 2.669166
#> iter  50 value 2.190129
#> iter  60 value 2.057145
#> iter  70 value 2.031552
#> iter  80 value 2.030720
#> iter  90 value 2.030692
#> final  value 2.030691 
#> converged
#> # weights:  13
#> initial  value 56.501349 
#> iter  10 value 4.546989
#> iter  20 value 2.412030
#> iter  30 value 2.211975
#> iter  40 value 2.126688
#> iter  50 value 2.118982
#> iter  60 value 2.118522
#> final  value 2.118318 
#> converged
#> # weights:  13
#> initial  value 1537.541660 
#> iter  10 value 45.893358
#> iter  20 value 14.179474
#> iter  30 value 6.293025
#> iter  40 value 2.966490
#> iter  50 value 2.250200
#> iter  60 value 2.200879
#> iter  70 value 2.132716
#> iter  80 value 2.116182
#> iter  90 value 2.113110
#> final  value 2.112921 
#> converged
#> # weights:  13
#> initial  value 3354.677303 
#> iter  10 value 8.207666
#> iter  20 value 5.979884
#> iter  30 value 4.402456
#> iter  40 value 2.680091
#> iter  50 value 2.140337
#> iter  60 value 2.120667
#> iter  70 value 2.090521
#> iter  80 value 2.072754
#> iter  90 value 2.064807
#> iter 100 value 2.063714
#> final  value 2.063714 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 1495.824272 
#> iter  10 value 6.518061
#> iter  20 value 4.118493
#> iter  30 value 3.189918
#> iter  40 value 2.385578
#> iter  50 value 2.157477
#> iter  60 value 2.139096
#> iter  70 value 2.136309
#> final  value 2.136306 
#> converged
#> # weights:  13
#> initial  value 11.757653 
#> iter  10 value 3.909688
#> iter  20 value 2.556194
#> iter  30 value 2.363998
#> iter  40 value 2.217477
#> iter  50 value 2.190203
#> iter  60 value 2.185572
#> iter  70 value 2.183208
#> final  value 2.183205 
#> converged
#> # weights:  13
#> initial  value 154.922979 
#> iter  10 value 5.007005
#> iter  20 value 2.986467
#> iter  30 value 2.324922
#> iter  40 value 2.096300
#> iter  50 value 2.077648
#> iter  60 value 2.071380
#> iter  70 value 2.070058
#> final  value 2.070057 
#> converged
#> # weights:  13
#> initial  value 1295.102618 
#> iter  10 value 20.587942
#> iter  20 value 5.648115
#> iter  30 value 4.498304
#> iter  40 value 2.651133
#> iter  50 value 2.284889
#> iter  60 value 2.195444
#> iter  70 value 2.167062
#> iter  80 value 2.151623
#> iter  90 value 2.147625
#> final  value 2.147598 
#> converged
#> # weights:  13
#> initial  value 6196.422374 
#> iter  10 value 9.791647
#> iter  20 value 8.194195
#> iter  30 value 5.683012
#> iter  40 value 2.600464
#> iter  50 value 2.259054
#> iter  60 value 2.197961
#> iter  70 value 2.156120
#> iter  80 value 2.116732
#> iter  90 value 2.099782
#> iter 100 value 2.096804
#> final  value 2.096804 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 165.586684 
#> iter  10 value 6.965082
#> iter  20 value 2.942559
#> iter  30 value 2.400000
#> iter  40 value 2.192173
#> iter  50 value 2.147873
#> iter  60 value 2.145626
#> iter  70 value 2.144777
#> final  value 2.144775 
#> converged
#> # weights:  13
#> initial  value 3685.490536 
#> iter  10 value 7.497643
#> iter  20 value 4.678847
#> iter  30 value 3.198315
#> iter  40 value 2.332407
#> iter  50 value 2.266814
#> iter  60 value 2.246946
#> iter  70 value 2.230340
#> iter  80 value 2.225874
#> iter  90 value 2.223878
#> final  value 2.223678 
#> converged
#> # weights:  13
#> initial  value 1883.675021 
#> iter  10 value 9.414955
#> iter  20 value 6.244387
#> iter  30 value 3.029821
#> iter  40 value 2.441478
#> iter  50 value 2.388556
#> iter  60 value 2.310839
#> iter  70 value 2.223355
#> iter  80 value 2.200783
#> iter  90 value 2.161414
#> iter 100 value 2.149199
#> final  value 2.149199 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 2896.671370 
#> iter  10 value 5.948826
#> iter  20 value 3.887106
#> iter  30 value 2.866152
#> iter  40 value 2.358066
#> iter  50 value 2.269247
#> iter  60 value 2.244193
#> iter  70 value 2.236110
#> iter  80 value 2.235692
#> final  value 2.235688 
#> converged
#> # weights:  13
#> initial  value 1160.170910 
#> iter  10 value 31.153142
#> iter  20 value 11.439016
#> iter  30 value 5.790787
#> iter  40 value 3.100087
#> iter  50 value 2.444872
#> iter  60 value 2.285386
#> iter  70 value 2.154482
#> iter  80 value 2.141414
#> iter  90 value 2.136232
#> final  value 2.135919 
#> converged
#> # weights:  13
#> initial  value 3189.626236 
#> iter  10 value 5.430796
#> iter  20 value 3.625953
#> iter  30 value 2.730844
#> iter  40 value 2.340266
#> iter  50 value 2.247853
#> iter  60 value 2.174153
#> iter  70 value 2.141220
#> iter  80 value 2.127328
#> iter  90 value 2.098656
#> iter 100 value 2.071428
#> final  value 2.071428 
#> stopped after 100 iterations
#> # weights:  13
#> initial  value 316.924838 
#> iter  10 value 5.937193
#> iter  20 value 4.755514
#> iter  30 value 3.663735
#> iter  40 value 2.233143
#> iter  50 value 2.134806
#> iter  60 value 2.113021
#> iter  70 value 2.101975
#> iter  80 value 2.100327
#> iter  90 value 2.100020
#> final  value 2.100013 
#> converged
#> # weights:  13
#> initial  value 1475.824755 
#> iter  10 value 6.897328
#> iter  20 value 5.017823
#> iter  30 value 3.550261
#> iter  40 value 2.277808
#> iter  50 value 2.126565
#> iter  60 value 2.103660
#> iter  70 value 2.089784
#> iter  80 value 2.089397
#> final  value 2.089397 
#> converged
#> # weights:  13
#> initial  value 2705.392001 
#> iter  10 value 25.983461
#> iter  20 value 9.945895
#> iter  30 value 4.266584
#> iter  40 value 3.251963
#> iter  50 value 2.661341
#> iter  60 value 2.218021
#> iter  70 value 2.117866
#> iter  80 value 2.104051
#> iter  90 value 2.101507
#> final  value 2.101324 
#> converged

# Try HessianMLP
NeuralSens::HessianMLP(caretmod)
#> Warning: All aesthetics have length 1, but the data has 3 rows.
#> ℹ Did you mean to use `annotate()`?
#> Warning: minimum occurred at one end of the range
#> Warning: minimum occurred at one end of the range

#> Sensitivity analysis of 2-3-1 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $.outcome
#> , , 1
#> 
#>                WD         TEMP
#> WD   0.0080548740 0.0006507174
#> TEMP 0.0006507174 0.0501312386
#> 
#> , , 2
#> 
#>                WD        TEMP
#> WD   -0.003715874 0.002293548
#> TEMP  0.002293548 0.058358834
#> 
#> , , 3
#> 
#>                WD        TEMP
#> WD   -0.005441919 0.002616204
#> TEMP  0.002616204 0.049183293
#> 
#> , , 4
#> 
#>                WD        TEMP
#> WD   -0.005505955 0.002723758
#> TEMP  0.002723758 0.032930386
#> 
#> , , 5
#> 
#>                WD        TEMP
#> WD   -0.005709236 0.002436998
#> TEMP  0.002436998 0.073151732
#> 

## Train h2o NNET --------------------------------------------------------------
# Create a cluster with 4 available cores
h2o::h2o.init(ip = "localhost",
              nthreads = 4)
#> 
#> H2O is not running yet, starting it now...
#> 
#> Note:  In case of errors look at the following log files:
#>     C:\Users\JPIZAR~1\AppData\Local\Temp\RtmpmwWafn\file16507ec44e0e/h2o_jpizarroso_started_from_r.out
#>     C:\Users\JPIZAR~1\AppData\Local\Temp\RtmpmwWafn\file16504fd83d73/h2o_jpizarroso_started_from_r.err
#> 
#> 
#> Starting H2O JVM and connecting:  Connection successful!
#> 
#> R is connected to the H2O cluster: 
#>     H2O cluster uptime:         3 seconds 87 milliseconds 
#>     H2O cluster timezone:       Europe/Madrid 
#>     H2O data parsing timezone:  UTC 
#>     H2O cluster version:        3.44.0.3 
#>     H2O cluster version age:    6 months and 4 days 
#>     H2O cluster name:           H2O_started_from_R_jpizarroso_inw091 
#>     H2O cluster total nodes:    1 
#>     H2O cluster total memory:   7.91 GB 
#>     H2O cluster total cores:    20 
#>     H2O cluster allowed cores:  4 
#>     H2O cluster healthy:        TRUE 
#>     H2O Connection ip:          localhost 
#>     H2O Connection port:        54321 
#>     H2O Connection proxy:       NA 
#>     H2O Internal Security:      FALSE 
#>     R Version:                  R version 4.3.3 (2024-02-29 ucrt) 
#> Warning: 
#> Your H2O cluster version is (6 months and 4 days) old. There may be a newer version available.
#> Please download and install the latest version from: https://h2o-release.s3.amazonaws.com/h2o/latest_stable.html
#> 

# Reset the cluster
h2o::h2o.removeAll()
fdata_h2o <- h2o::as.h2o(x = fdata.Reg.tr, destination_frame = "fdata_h2o")
#> 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |======================================================================| 100%

set.seed(150)
h2omod <-h2o:: h2o.deeplearning(x = names(fdata.Reg.tr)[2:ncol(fdata.Reg.tr)],
                                     y = names(fdata.Reg.tr)[1],
                                     distribution = "AUTO",
                                     training_frame = fdata_h2o,
                                     standardize = TRUE,
                                     activation = "Tanh",
                                     hidden = c(hidden_neurons),
                                     stopping_rounds = 0,
                                     epochs = iters,
                                     seed = 150,
                                     model_id = "nnet_h2o",
                                     adaptive_rate = FALSE,
                                     rate_decay = decay,
                                     export_weights_and_biases = TRUE)
#> 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |======================================================================| 100%

# Try HessianMLP
NeuralSens::HessianMLP(h2omod)
#> Error in value[[3L]](cond): The training data has not been detected, load the data to the h2o cluster

# Turn off the cluster
h2o::h2o.shutdown(prompt = FALSE)
rm(fdata_h2o)

## Train RSNNS NNET ------------------------------------------------------------
# Normalize data using RSNNS algorithms
trData <- as.data.frame(RSNNS::normalizeData(fdata.Reg.tr))
names(trData) <- names(fdata.Reg.tr)
set.seed(150)
RSNNSmod <-RSNNS::mlp(x = trData[,2:ncol(trData)],
                           y = trData[,1],
                           size = hidden_neurons,
                           linOut = TRUE,
                           learnFuncParams=c(decay),
                           maxit=iters)

# Try HessianMLP
NeuralSens::HessianMLP(RSNNSmod, trData = trData, output_name = "DEM")
#> Warning: All aesthetics have length 1, but the data has 3 rows.
#> ℹ Did you mean to use `annotate()`?

#> Sensitivity analysis of 2-5-1 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $DEM
#> , , 1
#> 
#>               WD       TEMP
#> WD   0.002575086 0.03535806
#> TEMP 0.035358060 1.15458447
#> 
#> , , 2
#> 
#>               WD       TEMP
#> WD   -0.61096374 0.06024617
#> TEMP  0.06024617 0.31091788
#> 
#> , , 3
#> 
#>               WD        TEMP
#> WD   -0.53952940 -0.02698437
#> TEMP -0.02698437 -0.78909969
#> 
#> , , 4
#> 
#>               WD        TEMP
#> WD   -0.53538154 -0.09282737
#> TEMP -0.09282737 -1.70730704
#> 
#> , , 5
#> 
#>              WD      TEMP
#> WD   -0.5105605 0.1222717
#> TEMP  0.1222717 1.3438703
#> 

## USE DEFAULT METHOD ----------------------------------------------------------
NeuralSens::HessianMLP(caretmod$finalModel$wts,
                            trData = fdata.Reg.tr,
                            mlpstr = caretmod$finalModel$n,
                            coefnames = caretmod$coefnames,
                            actfun = c("linear","sigmoid","linear"),
                            output_name = "DEM")
#> Warning: All aesthetics have length 1, but the data has 3 rows.
#> ℹ Did you mean to use `annotate()`?
#> Warning: minimum occurred at one end of the range

#> Sensitivity analysis of 2-3-1 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $DEM
#> , , 1
#> 
#>               WD        TEMP
#> WD   -0.00464978  0.00231262
#> TEMP  0.00231262 -0.03172112
#> 
#> , , 2
#> 
#>                WD         TEMP
#> WD   -0.005545458  0.002480041
#> TEMP  0.002480041 -0.031254782
#> 
#> , , 3
#> 
#>                WD         TEMP
#> WD   -0.005627625  0.002447588
#> TEMP  0.002447588 -0.032088962
#> 
#> , , 4
#> 
#>                WD         TEMP
#> WD   -0.005558544  0.002355347
#> TEMP  0.002355347 -0.033006047
#> 
#> , , 5
#> 
#>                WD         TEMP
#> WD   -0.005754328  0.002578274
#> TEMP  0.002578274 -0.029533354
#> 

################################################################################
#########################  CLASSIFICATION NNET #################################
################################################################################
## Regression dataframe --------------------------------------------------------
# Scale the data
fdata.Reg.cl <- fdata[,2:ncol(fdata)]
fdata.Reg.cl[,2:3] <- fdata.Reg.cl[,2:3]/10
fdata.Reg.cl[,1] <- fdata.Reg.cl[,1]/1000

# Normalize the data for some models
preProc <- caret::preProcess(fdata.Reg.cl, method = c("center","scale"))
nntrData <- predict(preProc, fdata.Reg.cl)

# Factorize the output
fdata.Reg.cl$DEM <- factor(round(fdata.Reg.cl$DEM, digits = 1))

# Normalize the data for some models
preProc <- caret::preProcess(fdata.Reg.cl, method = c("center","scale"))
nntrData <- predict(preProc, fdata.Reg.cl)

## Train caret NNET ------------------------------------------------------------
# Create trainControl
ctrl_tune <- caret::trainControl(method = "boot",
                                 savePredictions = FALSE,
                                 summaryFunction = caret::defaultSummary)
set.seed(150) #For replication
caretmod <- caret::train(form = DEM~.,
                                data = fdata.Reg.cl,
                                method = "nnet",
                                linout = FALSE,
                                tuneGrid = data.frame(size = hidden_neurons,
                                                      decay = decay),
                                maxit = iters,
                                preProcess = c("center","scale"),
                                trControl = ctrl_tune,
                                metric = "Accuracy")
#> # weights:  45
#> initial  value 3772.842618 
#> iter  10 value 1557.564302
#> iter  20 value 1214.199134
#> iter  30 value 1110.296648
#> iter  40 value 1070.982383
#> iter  50 value 1040.282432
#> iter  60 value 1026.243143
#> iter  70 value 1022.185164
#> iter  80 value 1018.932608
#> iter  90 value 1014.806386
#> iter 100 value 1012.499658
#> final  value 1012.499658 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 2668.172951 
#> iter  10 value 1496.742417
#> iter  20 value 1187.526898
#> iter  30 value 1050.272689
#> iter  40 value 1013.322223
#> iter  50 value 996.639753
#> iter  60 value 979.316887
#> iter  70 value 969.798307
#> iter  80 value 966.613930
#> iter  90 value 965.693488
#> iter 100 value 965.463123
#> final  value 965.463123 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3297.203342 
#> iter  10 value 1377.287449
#> iter  20 value 1112.310755
#> iter  30 value 1023.822455
#> iter  40 value 991.843628
#> iter  50 value 956.727170
#> iter  60 value 941.910334
#> iter  70 value 936.609226
#> iter  80 value 935.410703
#> iter  90 value 935.163698
#> iter 100 value 935.127337
#> final  value 935.127337 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3568.399296 
#> iter  10 value 1489.763894
#> iter  20 value 1219.257218
#> iter  30 value 1076.771253
#> iter  40 value 1024.503423
#> iter  50 value 998.708032
#> iter  60 value 981.840999
#> iter  70 value 973.720379
#> iter  80 value 971.090791
#> iter  90 value 968.967523
#> iter 100 value 968.494390
#> final  value 968.494390 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3003.535668 
#> iter  10 value 1439.044442
#> iter  20 value 1176.600696
#> iter  30 value 1048.481267
#> iter  40 value 1016.572547
#> iter  50 value 1011.297145
#> iter  60 value 999.404464
#> iter  70 value 988.451143
#> iter  80 value 977.282991
#> iter  90 value 972.906275
#> iter 100 value 971.896597
#> final  value 971.896597 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3408.995747 
#> iter  10 value 1341.622904
#> iter  20 value 1089.969900
#> iter  30 value 1029.207268
#> iter  40 value 996.486089
#> iter  50 value 988.952619
#> iter  60 value 976.464472
#> iter  70 value 972.214434
#> iter  80 value 970.881761
#> iter  90 value 969.641644
#> iter 100 value 969.485114
#> final  value 969.485114 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 4281.102149 
#> iter  10 value 1513.066785
#> iter  20 value 1329.056483
#> iter  30 value 1209.982389
#> iter  40 value 1118.764207
#> iter  50 value 1076.036468
#> iter  60 value 1061.718419
#> iter  70 value 1050.693937
#> iter  80 value 1040.872146
#> iter  90 value 1029.507488
#> iter 100 value 1025.374541
#> final  value 1025.374541 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3265.828022 
#> iter  10 value 1456.434584
#> iter  20 value 1166.808947
#> iter  30 value 1057.977863
#> iter  40 value 1008.996008
#> iter  50 value 978.114751
#> iter  60 value 970.985521
#> iter  70 value 966.104095
#> iter  80 value 963.006874
#> iter  90 value 962.094607
#> iter 100 value 961.841612
#> final  value 961.841612 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3019.717560 
#> iter  10 value 1333.523881
#> iter  20 value 1154.064664
#> iter  30 value 1067.529755
#> iter  40 value 1054.332888
#> iter  50 value 1049.493394
#> iter  60 value 1042.420751
#> iter  70 value 1025.594053
#> iter  80 value 1018.729658
#> iter  90 value 1016.946541
#> iter 100 value 1015.397734
#> final  value 1015.397734 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3405.760894 
#> iter  10 value 1597.431168
#> iter  20 value 1263.793552
#> iter  30 value 1114.159495
#> iter  40 value 1048.729401
#> iter  50 value 1023.871076
#> iter  60 value 976.998748
#> iter  70 value 960.770263
#> iter  80 value 954.884250
#> iter  90 value 952.488444
#> iter 100 value 951.344477
#> final  value 951.344477 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3013.688100 
#> iter  10 value 1535.862594
#> iter  20 value 1231.453772
#> iter  30 value 1132.096002
#> iter  40 value 1106.684078
#> iter  50 value 1083.676956
#> iter  60 value 1041.694085
#> iter  70 value 1032.125938
#> iter  80 value 1022.027396
#> iter  90 value 1006.266589
#> iter 100 value 1000.802958
#> final  value 1000.802958 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 4628.455991 
#> iter  10 value 1552.025703
#> iter  20 value 1211.906415
#> iter  30 value 1084.177292
#> iter  40 value 1064.063606
#> iter  50 value 1055.265752
#> iter  60 value 1049.279896
#> iter  70 value 1040.272607
#> iter  80 value 1038.639372
#> iter  90 value 1038.099537
#> iter 100 value 1037.787531
#> final  value 1037.787531 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 2860.694342 
#> iter  10 value 1511.390857
#> iter  20 value 1168.419352
#> iter  30 value 1094.111978
#> iter  40 value 1073.168803
#> iter  50 value 1069.749263
#> iter  60 value 1066.180221
#> iter  70 value 1064.629158
#> iter  80 value 1064.226117
#> iter  90 value 1063.853095
#> iter 100 value 1062.896671
#> final  value 1062.896671 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3377.433754 
#> iter  10 value 1446.109214
#> iter  20 value 1171.013957
#> iter  30 value 1114.422290
#> iter  40 value 1085.906251
#> iter  50 value 1056.654790
#> iter  60 value 1043.204252
#> iter  70 value 1039.982529
#> iter  80 value 1037.244251
#> iter  90 value 1036.464530
#> iter 100 value 1036.224249
#> final  value 1036.224249 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3253.715832 
#> iter  10 value 1411.560701
#> iter  20 value 1173.605210
#> iter  30 value 1141.598323
#> iter  40 value 1110.027489
#> iter  50 value 1075.678228
#> iter  60 value 1065.287014
#> iter  70 value 1061.607689
#> iter  80 value 1054.627824
#> iter  90 value 1034.673250
#> iter 100 value 1029.300197
#> final  value 1029.300197 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3863.665785 
#> iter  10 value 1387.778891
#> iter  20 value 1141.991241
#> iter  30 value 1113.544623
#> iter  40 value 1093.112775
#> iter  50 value 1064.466827
#> iter  60 value 1053.501083
#> iter  70 value 1035.802924
#> iter  80 value 1020.443915
#> iter  90 value 1015.693675
#> iter 100 value 1014.111725
#> final  value 1014.111725 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3378.665527 
#> iter  10 value 1400.194414
#> iter  20 value 1134.238327
#> iter  30 value 1072.434905
#> iter  40 value 1022.352730
#> iter  50 value 1009.326061
#> iter  60 value 1003.254602
#> iter  70 value 998.622585
#> iter  80 value 996.924622
#> iter  90 value 995.431517
#> iter 100 value 995.296204
#> final  value 995.296204 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3778.883814 
#> iter  10 value 1287.189554
#> iter  20 value 1085.911856
#> iter  30 value 1048.258887
#> iter  40 value 1031.285258
#> iter  50 value 1020.746772
#> iter  60 value 1009.982512
#> iter  70 value 1001.117193
#> iter  80 value 996.249854
#> iter  90 value 995.002293
#> iter 100 value 994.464160
#> final  value 994.464160 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3120.123677 
#> iter  10 value 1354.765028
#> iter  20 value 1127.326225
#> iter  30 value 1030.192879
#> iter  40 value 995.812629
#> iter  50 value 987.332787
#> iter  60 value 980.506578
#> iter  70 value 976.439833
#> iter  80 value 975.171226
#> iter  90 value 974.762849
#> iter 100 value 974.669379
#> final  value 974.669379 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 4498.743913 
#> iter  10 value 1444.335556
#> iter  20 value 1196.519410
#> iter  30 value 1099.018244
#> iter  40 value 1029.077344
#> iter  50 value 1005.258084
#> iter  60 value 997.634916
#> iter  70 value 996.394696
#> iter  80 value 995.712015
#> iter  90 value 995.645881
#> iter 100 value 995.634593
#> final  value 995.634593 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 4178.969476 
#> iter  10 value 1484.773196
#> iter  20 value 1236.558325
#> iter  30 value 1131.376400
#> iter  40 value 1058.462683
#> iter  50 value 1018.919757
#> iter  60 value 1006.929988
#> iter  70 value 1000.924164
#> iter  80 value 997.057751
#> iter  90 value 992.146696
#> iter 100 value 990.467451
#> final  value 990.467451 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3763.027227 
#> iter  10 value 1502.580970
#> iter  20 value 1286.900665
#> iter  30 value 1169.576206
#> iter  40 value 1122.939531
#> iter  50 value 1108.972049
#> iter  60 value 1104.953532
#> iter  70 value 1103.270073
#> iter  80 value 1101.645238
#> iter  90 value 1098.946203
#> iter 100 value 1095.719635
#> final  value 1095.719635 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3634.283962 
#> iter  10 value 1393.174055
#> iter  20 value 1064.065558
#> iter  30 value 998.290332
#> iter  40 value 973.809987
#> iter  50 value 963.302264
#> iter  60 value 949.245382
#> iter  70 value 943.582074
#> iter  80 value 942.712725
#> iter  90 value 942.090755
#> iter 100 value 941.998670
#> final  value 941.998670 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 4122.006202 
#> iter  10 value 1440.624472
#> iter  20 value 1201.124592
#> iter  30 value 1081.368683
#> iter  40 value 1019.710036
#> iter  50 value 998.220181
#> iter  60 value 991.313592
#> iter  70 value 988.455638
#> iter  80 value 986.674128
#> iter  90 value 985.122136
#> iter 100 value 984.455611
#> final  value 984.455611 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3169.917474 
#> iter  10 value 1708.163015
#> iter  20 value 1275.618128
#> iter  30 value 1086.379758
#> iter  40 value 1017.730370
#> iter  50 value 994.236230
#> iter  60 value 984.400401
#> iter  70 value 982.537214
#> iter  80 value 981.070886
#> iter  90 value 980.488255
#> iter 100 value 980.416752
#> final  value 980.416752 
#> stopped after 100 iterations
#> # weights:  45
#> initial  value 3805.876854 
#> iter  10 value 1440.491291
#> iter  20 value 1164.498683
#> iter  30 value 1068.693224
#> iter  40 value 1030.794446
#> iter  50 value 1012.456002
#> iter  60 value 1005.801464
#> iter  70 value 1003.516310
#> iter  80 value 1002.997394
#> iter  90 value 1002.812312
#> iter 100 value 1002.764592
#> final  value 1002.764592 
#> stopped after 100 iterations

# Try HessianMLP
NeuralSens::HessianMLP(caretmod)
#> Warning: All aesthetics have length 1, but the data has 3 rows.
#> ℹ Did you mean to use `annotate()`?
#> Warning: minimum occurred at one end of the range

#> Sensitivity analysis of 2-5-5 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $X0.6
#> , , 1
#> 
#>             WD     TEMP
#> WD   -4.670997 5.172555
#> TEMP -4.879342 5.640700
#> 
#> , , 2
#> 
#>             WD      TEMP
#> WD   -1.989823 -3.100539
#> TEMP  4.604024  5.368306
#> 
#> , , 3
#> 
#>             WD      TEMP
#> WD   -2.164994 -2.821268
#> TEMP  4.745238  4.965177
#> 
#> , , 4
#> 
#>             WD      TEMP
#> WD   -2.059171 -2.542789
#> TEMP  4.353979  4.768402
#> 
#> , , 5
#> 
#>              WD        TEMP
#> WD   -0.6950128  0.08701548
#> TEMP  2.0283312 -0.15713481
#> 
#> $X0.7
#> , , 1
#> 
#>             WD     TEMP
#> WD   -4.879342 2.125629
#> TEMP -5.349701 2.370279
#> 
#> , , 2
#> 
#>             WD      TEMP
#> WD    4.604024 -1.335003
#> TEMP -6.963008 -2.934393
#> 
#> , , 3
#> 
#>             WD      TEMP
#> WD    4.745238 -2.758534
#> TEMP -7.137206 -5.365716
#> 
#> , , 4
#> 
#>             WD      TEMP
#> WD    4.353979 -2.435074
#> TEMP -6.712240 -4.405385
#> 
#> , , 5
#> 
#>             WD      TEMP
#> WD    2.028331 -1.676425
#> TEMP -2.032015 -5.638907
#> 
#> $X0.8
#> , , 1
#> 
#>            WD     TEMP
#> WD   1.800258 2.370279
#> TEMP 1.792172 2.685159
#> 
#> , , 2
#> 
#>             WD      TEMP
#> WD   0.8402014 -2.934393
#> TEMP 3.4258523 -2.048769
#> 
#> , , 3
#> 
#>            WD      TEMP
#> WD   2.517725 -5.365716
#> TEMP 6.356315 -4.476028
#> 
#> , , 4
#> 
#>            WD      TEMP
#> WD   2.163635 -4.405385
#> TEMP 5.357798 -4.079587
#> 
#> , , 5
#> 
#>            WD      TEMP
#> WD   1.498457 -5.638907
#> TEMP 6.115961 -2.092491
#> 
#> $X0.5
#> , , 1
#> 
#>            WD      TEMP
#> WD   1.792172 -4.159239
#> TEMP 1.697777 -4.457715
#> 
#> , , 2
#> 
#>            WD      TEMP
#> WD   3.425852  3.013873
#> TEMP 1.632748 -1.992721
#> 
#> , , 3
#> 
#>            WD      TEMP
#> WD   6.356315  3.729933
#> TEMP 4.623315 -2.913048
#> 
#> , , 4
#> 
#>            WD      TEMP
#> WD   5.357798  3.538264
#> TEMP 4.108822 -2.762054
#> 
#> , , 5
#> 
#>            WD      TEMP
#> WD   6.115961  3.874222
#> TEMP 2.727358 -2.592702
#> 
#> $X0.9
#> , , 1
#> 
#>            WD      TEMP
#> WD   4.902325 -4.457715
#> TEMP 5.172555 -4.676172
#> 
#> , , 2
#> 
#>              WD      TEMP
#> WD   -0.5312368 -1.992721
#> TEMP -3.1005392  2.004980
#> 
#> , , 3
#> 
#>             WD      TEMP
#> WD   -1.326780 -2.913048
#> TEMP -2.821268  2.017951
#> 
#> , , 4
#> 
#>             WD      TEMP
#> WD   -1.210080 -2.762054
#> TEMP -2.542789  1.908331
#> 
#> , , 5
#> 
#>               WD      TEMP
#> WD   -3.00259510 -2.592702
#> TEMP  0.08701548  1.551614
#> 

## Train h2o NNET --------------------------------------------------------------
# Create local cluster with 4 available cores
h2o::h2o.init(ip = "localhost",
              nthreads = 4)
#> 
#> H2O is not running yet, starting it now...
#> 
#> Note:  In case of errors look at the following log files:
#>     C:\Users\JPIZAR~1\AppData\Local\Temp\RtmpmwWafn\file165041d143da/h2o_jpizarroso_started_from_r.out
#>     C:\Users\JPIZAR~1\AppData\Local\Temp\RtmpmwWafn\file1650384212f2/h2o_jpizarroso_started_from_r.err
#> 
#> 
#> Starting H2O JVM and connecting:  Connection successful!
#> 
#> R is connected to the H2O cluster: 
#>     H2O cluster uptime:         2 seconds 741 milliseconds 
#>     H2O cluster timezone:       Europe/Madrid 
#>     H2O data parsing timezone:  UTC 
#>     H2O cluster version:        3.44.0.3 
#>     H2O cluster version age:    6 months and 4 days 
#>     H2O cluster name:           H2O_started_from_R_jpizarroso_vno719 
#>     H2O cluster total nodes:    1 
#>     H2O cluster total memory:   7.91 GB 
#>     H2O cluster total cores:    20 
#>     H2O cluster allowed cores:  4 
#>     H2O cluster healthy:        TRUE 
#>     H2O Connection ip:          localhost 
#>     H2O Connection port:        54321 
#>     H2O Connection proxy:       NA 
#>     H2O Internal Security:      FALSE 
#>     R Version:                  R version 4.3.3 (2024-02-29 ucrt) 
#> Warning: 
#> Your H2O cluster version is (6 months and 4 days) old. There may be a newer version available.
#> Please download and install the latest version from: https://h2o-release.s3.amazonaws.com/h2o/latest_stable.html
#> 

# Reset the cluster
h2o::h2o.removeAll()
fdata_h2o <- h2o::as.h2o(x = fdata.Reg.cl, destination_frame = "fdata_h2o")
#> 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |======================================================================| 100%

set.seed(150)
h2omod <- h2o::h2o.deeplearning(x = names(fdata.Reg.cl)[2:ncol(fdata.Reg.cl)],
                                       y = names(fdata.Reg.cl)[1],
                                       distribution = "AUTO",
                                       training_frame = fdata_h2o,
                                       standardize = TRUE,
                                       activation = "Tanh",
                                       hidden = c(hidden_neurons),
                                       stopping_rounds = 0,
                                       epochs = iters,
                                       seed = 150,
                                       model_id = "nnet_h2o",
                                       adaptive_rate = FALSE,
                                       rate_decay = decay,
                                       export_weights_and_biases = TRUE)
#> 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |======================================================================| 100%

# Try HessianMLP
NeuralSens::HessianMLP(h2omod)
#> Error in value[[3L]](cond): The training data has not been detected, load the data to the h2o cluster

# Apaga el cluster
h2o::h2o.shutdown(prompt = FALSE)
rm(fdata_h2o)

## TRAIN nnet NNET --------------------------------------------------------
# Create a formula to train NNET
form <- paste(names(fdata.Reg.tr)[2:ncol(fdata.Reg.tr)], collapse = " + ")
form <- formula(paste(names(fdata.Reg.tr)[1], form, sep = " ~ "))

set.seed(150)
nnetmod <- nnet::nnet(form,
                      data = nntrData,
                      linear.output = TRUE,
                      size = hidden_neurons,
                      decay = decay,
                      maxit = iters)
#> # weights:  45
#> initial  value 3571.076907 
#> iter  10 value 1391.280224
#> iter  20 value 1195.078969
#> iter  30 value 1148.503871
#> iter  40 value 1071.086906
#> iter  50 value 1016.236754
#> iter  60 value 1003.803225
#> iter  70 value 998.327935
#> iter  80 value 996.114736
#> iter  90 value 995.001087
#> iter 100 value 994.799975
#> final  value 994.799975 
#> stopped after 100 iterations
# Try HessianMLP
NeuralSens::HessianMLP(nnetmod, trData = nntrData)
#> Warning: All aesthetics have length 1, but the data has 3 rows.
#> ℹ Did you mean to use `annotate()`?
#> Warning: minimum occurred at one end of the range

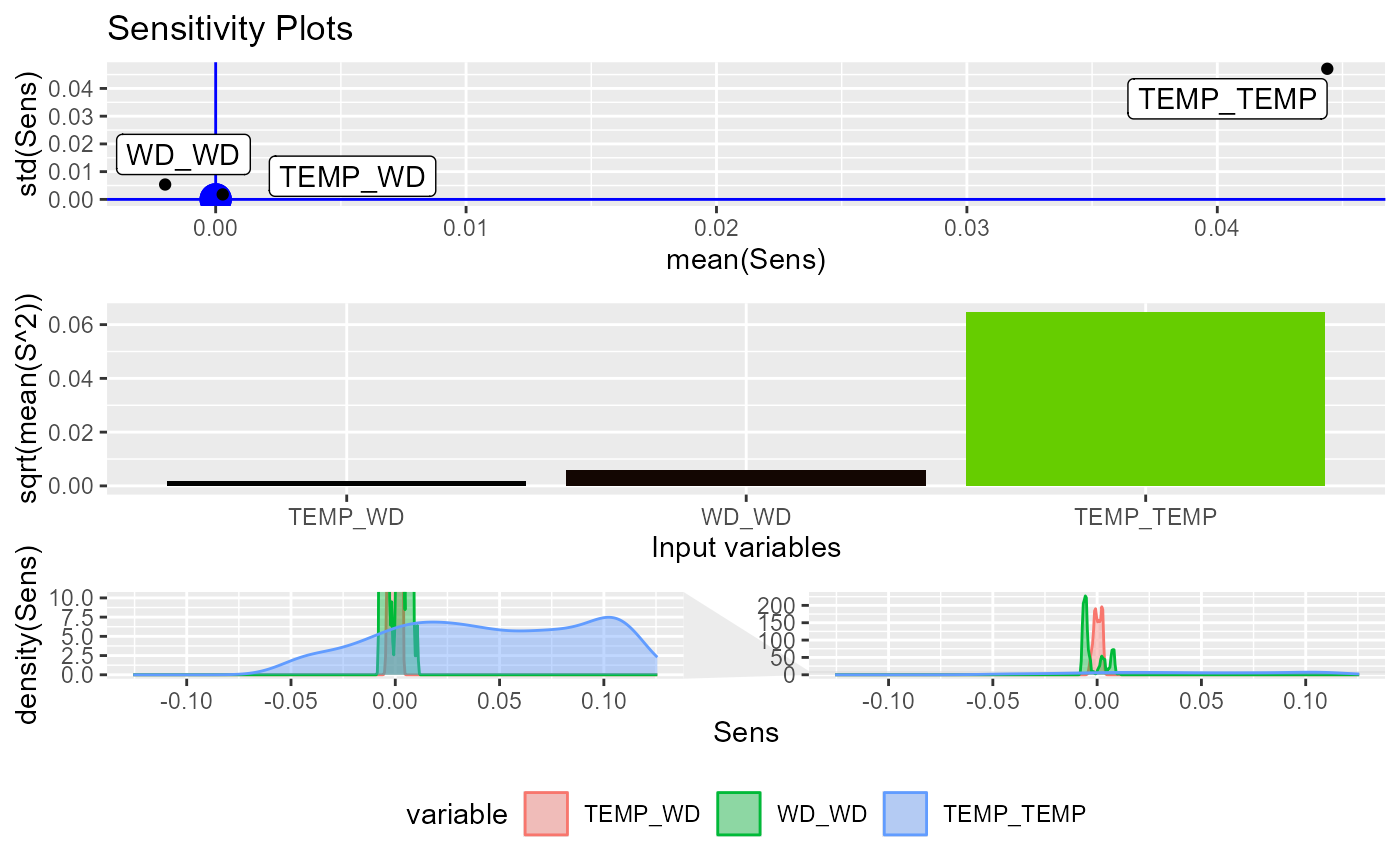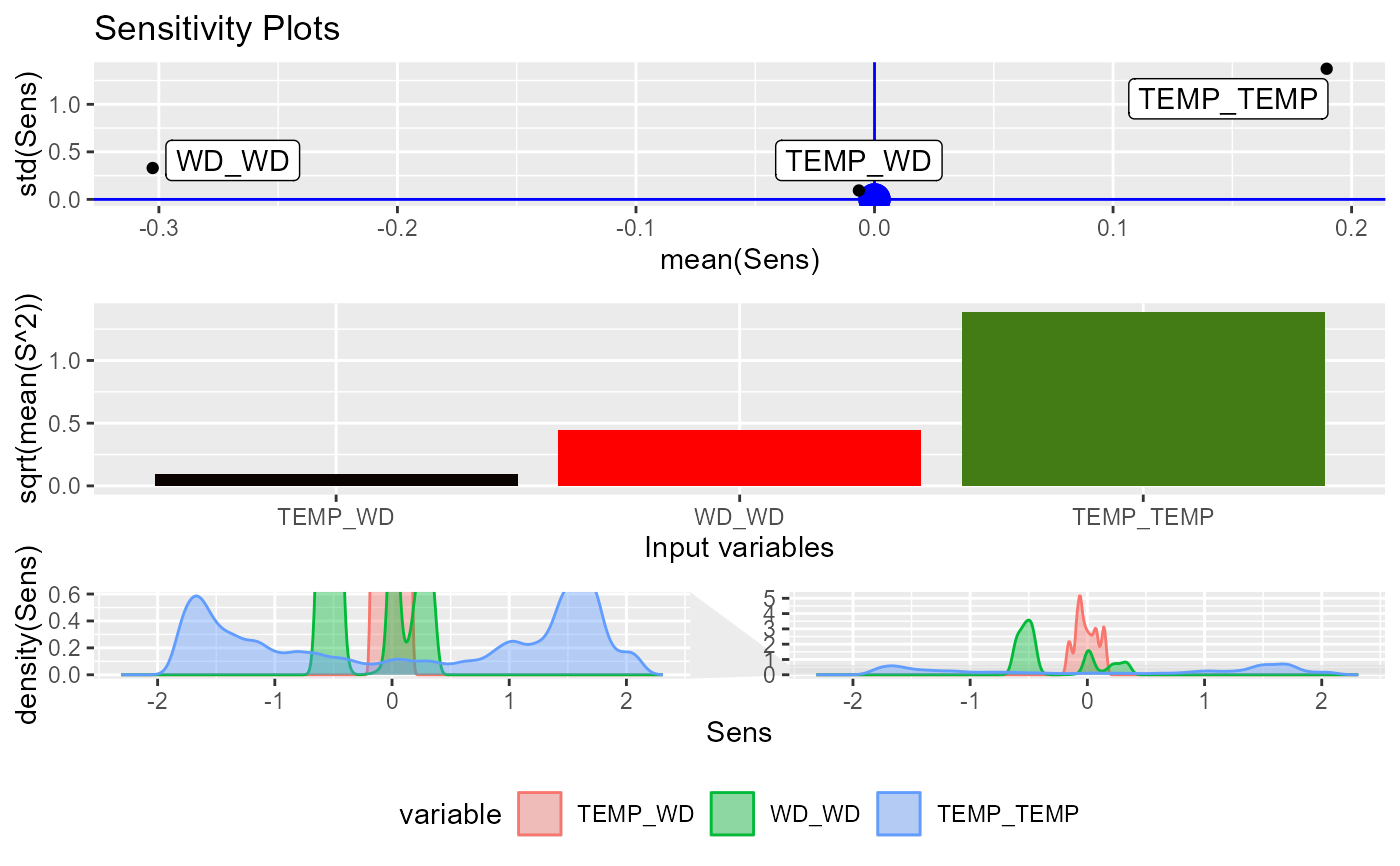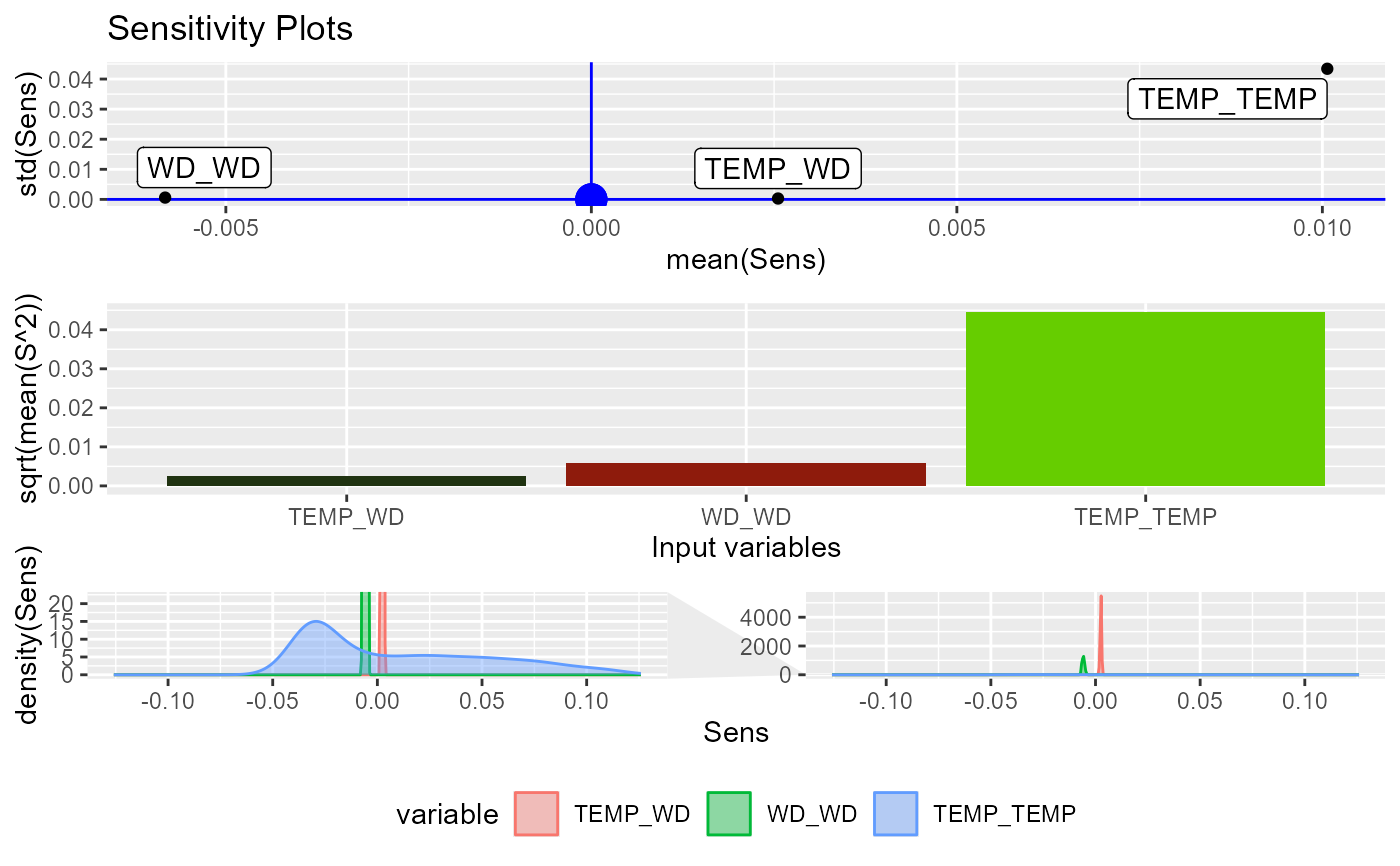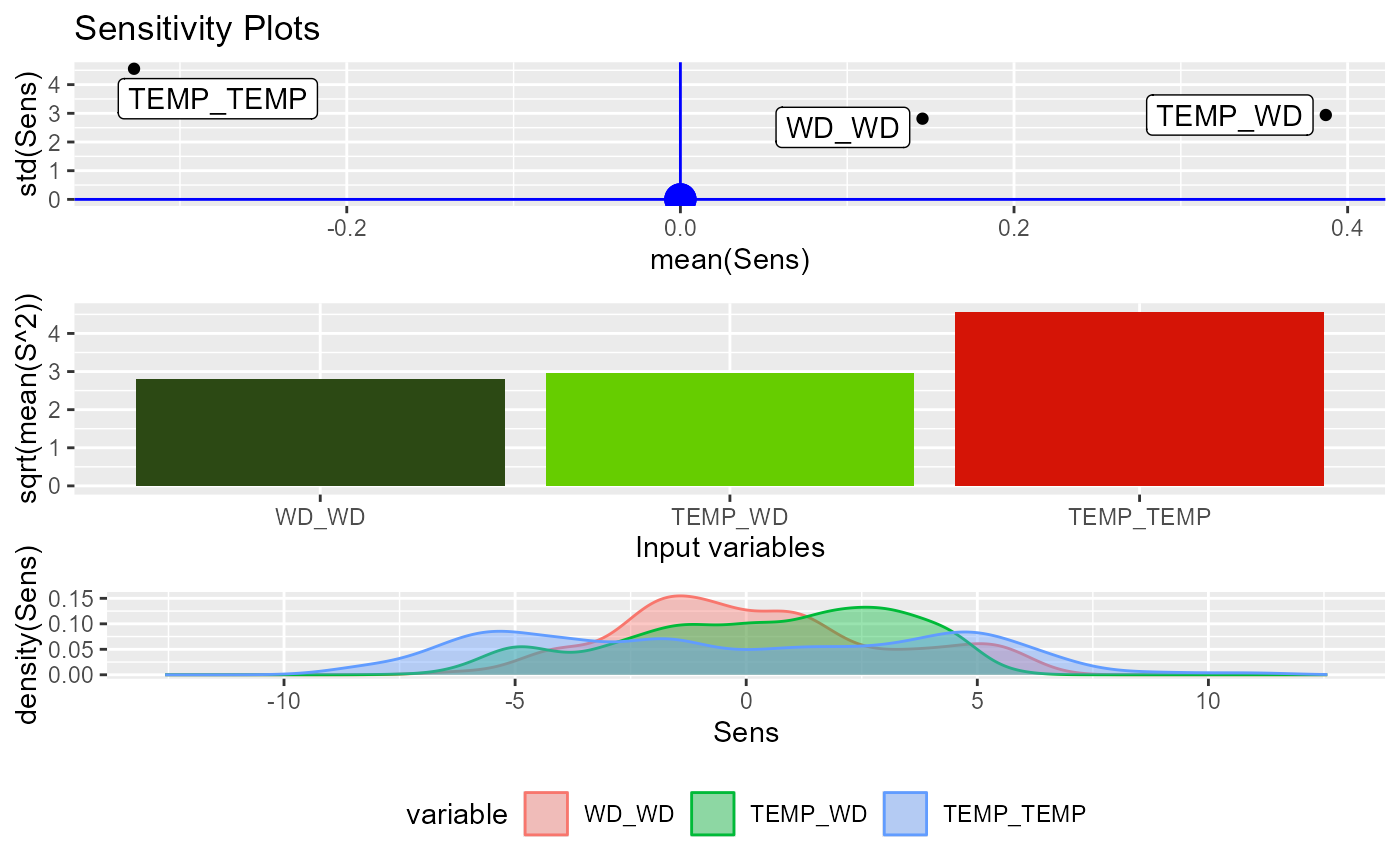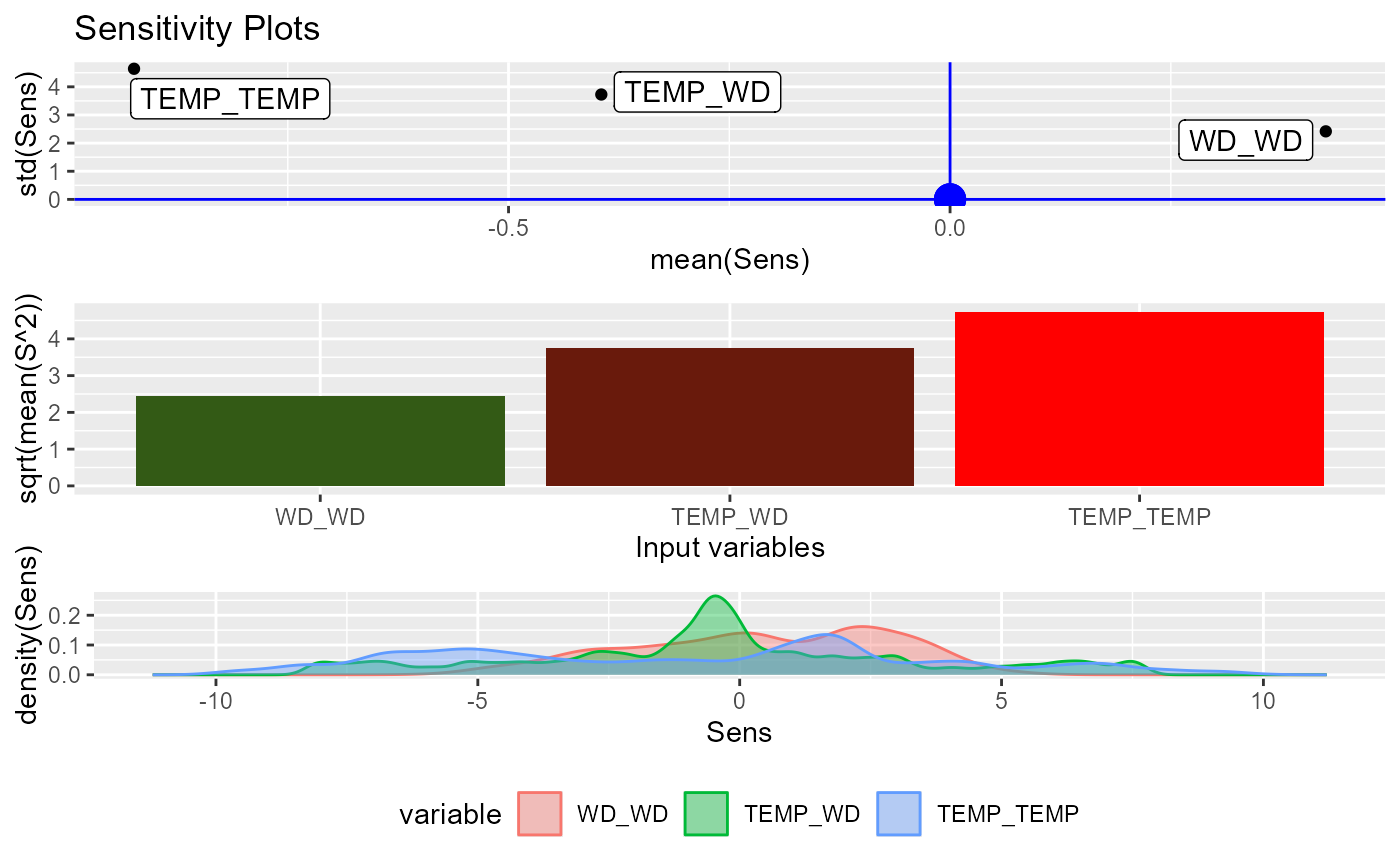#> Sensitivity analysis of 2-5-5 MLP network.
#> 
#>   1980 samples
#> 
#> Sensitivities of each output (only 5 first samples):
#> $X0.6
#> , , 1
#> 
#>             WD     TEMP
#> WD   -4.704517 4.545073
#> TEMP -5.204573 8.204524
#> 
#> , , 2
#> 
#>            WD      TEMP
#> WD   3.636482 -1.520392
#> TEMP 1.402979 -1.715242
#> 
#> , , 3
#> 
#>             WD      TEMP
#> WD   1.9366770 0.7298632
#> TEMP 0.4339409 2.0236421
#> 
#> , , 4
#> 
#>               WD     TEMP
#> WD    1.84696744 0.893106
#> TEMP -0.05131954 1.886014
#> 
#> , , 5
#> 
#>            WD       TEMP
#> WD   2.039427 -0.8577403
#> TEMP 1.823289  0.6838412
#> 
#> $X0.7
#> , , 1
#> 
#>              WD      TEMP
#> WD    -5.204573 2.0904945
#> TEMP -10.231372 0.8312931
#> 
#> , , 2
#> 
#>            WD       TEMP
#> WD   1.402979 -2.8512509
#> TEMP 2.042167 -0.4214128
#> 
#> , , 3
#> 
#>              WD      TEMP
#> WD    0.4339409 -5.388502
#> TEMP -0.3122699 -5.900168
#> 
#> , , 4
#> 
#>               WD      TEMP
#> WD   -0.05131954 -4.923406
#> TEMP -0.28683943 -4.889934
#> 
#> , , 5
#> 
#>              WD      TEMP
#> WD    1.8232888 -3.272029
#> TEMP -0.4317642 -3.748964
#> 
#> $X0.8
#> , , 1
#> 
#>               WD      TEMP
#> WD   -0.93161275 0.8312931
#> TEMP -0.09548594 2.3962172
#> 
#> , , 2
#> 
#>             WD       TEMP
#> WD   1.5124632 -0.4214128
#> TEMP 0.2533784 -0.1304020
#> 
#> , , 3
#> 
#>            WD      TEMP
#> WD   3.794342 -5.900168
#> TEMP 4.618171 -7.902479
#> 
#> , , 4
#> 
#>            WD      TEMP
#> WD   3.438228 -4.889934
#> TEMP 3.886478 -7.157341
#> 
#> , , 5
#> 
#>            WD      TEMP
#> WD   2.151412 -3.748964
#> TEMP 2.769673 -2.309080
#> 
#> $X0.5
#> , , 1
#> 
#>               WD       TEMP
#> WD   -0.09548594  0.6732030
#> TEMP -0.66859269 -0.2025328
#> 
#> , , 2
#> 
#>              WD       TEMP
#> WD    0.2533784 -1.2382507
#> TEMP -0.1375629  0.3305278
#> 
#> , , 3
#> 
#>            WD        TEMP
#> WD   4.618171 -0.84941369
#> TEMP 6.214149  0.09189471
#> 
#> , , 4
#> 
#>            WD       TEMP
#> WD   3.886478 -0.8679072
#> TEMP 5.620583  0.1327155
#> 
#> , , 5
#> 
#>            WD        TEMP
#> WD   2.769673 -0.66905624
#> TEMP 1.876398  0.03313204
#> 
#> $X0.9
#> , , 1
#> 
#>            WD        TEMP
#> WD   2.806829 -0.20253282
#> TEMP 4.545073  0.07869205
#> 
#> , , 2
#> 
#>             WD         TEMP
#> WD   -1.050304  0.330527772
#> TEMP -1.520392 -0.009908438
#> 
#> , , 3
#> 
#>             WD        TEMP
#> WD   0.4758575  0.09189471
#> TEMP 0.7298632 -0.08771664
#> 
#> , , 4
#> 
#>             WD       TEMP
#> WD   0.4755354  0.1327155
#> TEMP 0.8931060 -0.1235752
#> 
#> , , 5
#> 
#>              WD       TEMP
#> WD   -0.2561691 0.03313204
#> TEMP -0.8577403 0.16450131
#> 
# }